Course / training:Method for Logical AnalysisPrinciples of Formal logic.Combinatory Explosion in Logical SystemsContents
1. Introduction
: Information, logic and complexity.
1.a. Foundationsof a Logical system 1.b. Starting parameters 2. Semantic expansion.
2.1. Elementary object states.
2.2. Domain states. 2.3. Logical relations. 2.4. Truth values table. 2.5. Arguments (Semantic). 2.6. Inference schemes (Syntactic). 2.7. Inferences, derivations (Semantic). Combinatory Explosion in Logical Systems1.Introduction:the emergence of a System of Logic.Judgment makes use of information.Our judgments and estimations are in many ways like our other reactions and decisions. They are based on information we have available - at conscious as well as subconscious levels. Information and difference.About the concept of 'information' a lot of different views and understands exist. To avoid misunderstandings, and grasp its essential meaning, it's useful to first look at its most characteristicproperty. This becomes apparant when we try to conceive of a situation where she is totally absent. Clearly, without any information there is only utter chaos, senseless 'noise', total vagueness, a completely non-knowing. Information only comes into play with the perception of any difference. As soon as a distinction can be made - eg a difference between on/off, in/out, true/false, etc. - some order emerges. Only then reasoning becomes possible, and logic applies. Every amount of information thus implies at least one difference. Information and ordering.Any difference on its turn implies at least two'things', phenomena or states in an area in reality. Thus, based on distinctions, combinationsof things can be be considered. Between these things simultaneously exists at least one order, ie the one that necessarily follows from their difference as perceived. Moreover, in order to make any sense to us, information in general can not purely consist of loose data. We view the information in a certain cohesion. This implies that it allows for some ordering to be distinguished. Viewed in reverse, every ordered state, or structure, represents in itself a certain amount of information. Logical relations.Given a random collection of elements, we may take a look at the logical relations that are possible between those elements. The logical relations refer to the range of states or values which the elements can take seperately, as well as through their mutual derivation relations. Information and reasoning.By combining data, we may obtain more complex forms of information. Naturally, we do this by means of our thinking. Every train of thought, and in fact every process of information processing, has the general form of a reasoning, that is to say:
Reasoning:
The ways in which those combinations can be made, and the values that these combinations can take, are determined by the laws of
logic.A number of input data are combined, and next certain data are derived from the combination. Of course these properties certainly apply to judgments and estimations. They are to be considered as reasonings, in that they operate on certain information, and produce information thereafter. Laws of logic.The logical laws only apply to the relationsbetween data, ie the combinations and derivations, and not to the individual data (such as direct observations and feelings). They also apply independentlyof the content and the natureof the data, which includes possible variations in subject, domain, problem, purpose, application, scope, etc.. Levelsof logical complexity.Each form of reasoning, or argument, consists of a combination of one or more distinct logical relations. Orderings, and therefore arguments, are possible in every imaginable form, but also in every unthinkableform: they are virtually unlimited in possible variation, complexity and size. As will be show below, in a few steps this already reaches far beyond the limits of the imagination and comprehension of people, and even beyond the capacities of calculation and data storage of physical and even theoretical computers of any conceivable size. Fortunenately, all of these possible forms can be sorted out en judged with help of the laws of logic. Therefore, understanding the laws of logic is indispensable for every judgment being meaningful and reliable. For the optimal use of logic, a clear understanding of the minimallevels of logical complexity and their proportions is indispensable. 1.a.Foundations of a Logical system.In this overview we look at the logical possibilities that follow from an arbitrary collection units (itemsor objects ). We'll see in what ways combinatorial explosion occurs, to what extent this happens and what consequences it has for the complexity of information processing and judgment regarding the input data. To limit ourselves to the most generally valid principles we will focus on a logical system which itself is of minimal complexity . From this system, propositionlogic can be derived, but also, with the necessary additions, more complex systems such as predicate logic and modal logic. In general applies that the consequences of combinatorial explosion and complexity themselves increase in explosiveways with each degree of increasing refinement of the logical system which we apply. Logical system at semanticlevel.S!: a logicalsystem ('apparatus', calculus).S!PPL:S!is a system in propositional logic (PPL) (or higher).S!PDL-I:S!is a system in predicate logic (PDL-I), first-order logic (FOL) (or higher).S!) : the semantics, a set of ordering rules, ofS!.Logical system at syntacticallevel.L!: a formal system (language system).L!PPL:L!is a language/system in propositional logic(or higher).L!PDL-I:L!is a language/system in predicate logic, first-order logic ,FOL, (or higher).L!) : the syntaxis, or grammer, a set of ordering rules, ofL!.WFF*( L!)) : the set of well-formed statements (formulas) ofL!.1.b.Starting parameters.1.1.Objects.Applicable in PPLand further.D*: (referential) domainor population, set of elements d[i]; with (i=1, .. d).d: domain- or population-size; total number of objects, domain-elements ('things', phenomena, items, variables) d[i] within D*.D*={d[1], .. d[i], .. d[d] }.d =|D*|.Example.With two items (d =2 ), the setD·d may consist of the following elements (objects), represented by proposition symbols and stated in arbitrary order: { (d { (d=2 ) ( (D·d={' A' ,' B'} ) }.S![s1] however extremely minimal, if not futile.Some examples of statements in such a 'minimal' system, stated in a formal language:
{ (d
Likewise, the domainmay consist of only one element. But then the inference systems =0 ) ( (D·d={} ) : ({}=(v){}); (({})$=(v)$0); ( {}=(r)$0); etc.}.S![s1 ] also remains very simple.Some examples of statements in such a 'primitive' system, stated in a formal language:
{ (d
=1 ) ( (D*={d [1]} ) : ((d[1])$=(v)$1); ((d[1])$=(v)$0); etc.}.Range.When the number of objects is less then one, any reasoning becomes meaningless. On the other hand, when it is infinite, an inconceivable amount of reasoning concerning the domain becomes practically undecidable. For a domainwhich is manageable, the following applies:
{ (d
=|D*(mgb)|); (1 (1 ≤d< 0 ) }.
0 ) }.1.2.Values.Generally applicative to objects. V*: value system or 'value palette', set of values v[j]; waarbij (j=1, ..v).v: total number of values, state values, object values or signal values (valences ); e.g. truth values, v[j] in V*.V*={v[1], .. v[j], .. v[v] }.v =|V*|.Example.With two values (v =2 ) the setV·v may consist of the following elements (values), represented by value constants and stated in arbitrary order: { (v { (v=2 ) ( (V·v={0 ,1} ) }.Range.When the number of values is less then two, any assignment of value becomes meaningless, and thus any attempt to meaningful reasoning becomes impossible. On the other hand, when this number is infinite, almost any reasoning concerning the domain becomes practically undecidable. For a value setwhich is sensible and manageable, the following applies:
{ (v
In =|V*(mgb)|); (2 (2 ≤v< 0 ) }.
0 ) }.PDLsome further parameters come into play.
(2a) p: total number of predicate-variables (attributes, predicate names); including identity, '='.
The (maximum) number of items a in (2b) r(v,d) : (maximum) number of argument-places, or arity, for each predicate name. (We may eventually use for simplicity and security the maximum over all predicate names). (2c) n: total number of elements (individuals, objects) in the referential domain (the population). PDLis a derivate of the latter three. {p {p ≤a≤(p*MAX(1,(r (v,d)*n)) }.PDLsystem we have sufficient information about the parameters p, r (v,d) and n, we can calculate a, and may reason further following the rules for aPPLsystem.Below we explore which combinatorial possibilities are generated by these parameters on the semanticlevel and the syntactic level respectively. 2.Semantic expansion .2.1.Elementary object states .Object states constitute pairs or tupels (the Cartesisch product) from the vvalues and delements. They reflect the domain at an observationallevel. At a semanticallevel these are truth statements with respect to separate objects. In logical language these are e.g. literals, ground instances, or 'witnesses'. They resemble samples from a population. H·(v,d): The set of all possible unique object states.Example.With two truth values(v =2, binary system) and two items(d=2) the setH·(v,d) may consist of the following elements (object states), represented by proposition symbols and stated in arbitrary order: ( (H·(v=2,d=2)={' A' ,'¬A' ,' B' ,'¬B' } ).Size.h(v,d): The total number of possible unique object states.  { {  v v  d
( h(v,d) d
( h(v,d) :=|H·(v,d)|;:= ( (|V·v|,|D·d|;:=v*d )d, v }.In a binarysystem.Under (v =2 ) applies:H·(v,d) is just as large as the doubling of setD·d.The values h(2,d) largely correspond to the sequence A005843 (formerly M0985) in the On-line Encyclopedia of Integer Sequences (OEIS).  { {  d( h(2,d) d( h(2,d) :=2*d;:=A005843(d)|(offset0 ) )d }.
Eg., from (d
={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );follows (h(2,d) ={ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,..}.Range.The number h(v,d) remains liniar (polynomial) in d.  (2 (2 ≤h(v,d)< 0 ).
0 ).Complexity class.The set H·(v,d) remains within the class of countable infinite sets (denumerable sets).Thus it can be searched algorithmically (it is tracktable) - with a singletape Turing machine- in linear polynomial computational time ( P-TIME). ( (H·(v,d)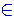
POLY(d^1);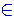 TIME(d);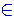
P-TIME).2.2.Domain states.Domain states consist of conjunctcombinations of all objects with their specific values, ie various object states . They reflect the domain in a purely descriptiveway. At a semanticallevel these are truth statements with respect to the state of the entire domain. They are similar to the cells (categories of variance) in a so-called contingency table (cross tabulation , of 'crosstab'), which forms the basis of numerous statistical measures for the comparision of variances, in particular Chi-square(Χ2), and variants or derivates of the latter, such as correlationcoefficient, regressioncoefficient, Student'st, F, Fisherz, etc.. B·(v,d): The set of all possible unique domain states.Example.With two truth values(v =2, binary system) and two items(d=2) the setB·(v,d) may consist of the following elements (domain states), represented by proposition symbols and stated in arbitrary order: ( (B·(v=2,d=2)={'( A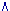 B)' ,'( A B)' ,'( A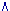 ¬B)' ,'(¬A
¬B)' ,'(¬A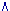 B)' ,'(¬A B)' ,'(¬A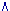 ¬B
)' } ). ¬B
)' } ).Size.b(v,d): The total number of possible unique domain states. The number b(v,d) equals the number of repetition variantions, or, sequence variations with replacement i.e. repetition, with size (length) d from velements.  { {  v v  d
( b(v,d) d
( b(v,d) :=|B·(v,d)|;:= (d1:=1, (d1:=1, ..d)v ;=v^d;:=b(v,d-1 )*v )d, v }.It is equal to the number of rows in the truth-values table. In a binarysystem.Under (v =2 ) applies:B·(v,d) is just as large as the set of all possible subsets - the power set - ofD·d.In a binarysystem the number of domain states represents the quantity of signal, signal content, or signal capacity , which is measured as the amount of domain elementsd in bits (binary digits): The values b(2,d) correspond to the sequence A000079 (formerly M1129, N0432) in the OEIS. I.e.:  { {  d( b(2,d) d( b(2,d) :=|P·d|;:=b(2,d -1 )*2;:=lg2dbits;:=A000079(d)|(offset0 ) )d }.
Eg., from (d
={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );follows (b(2,d) ={ 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,..} ).Range.The number b(v,d) remains exponential in d.  (2 (2 ≤b(v,d)< 0 ^
0 ^ 0 ); 0 );
Complexity class.The set B·(v,d) remains within the class of uncountable infinite sets , which have the size of the continuum (cardinality of the continuum).Thus it can only be searched algorthmically in exponential computational time ( EXP-TIME). ( (B·(v,d)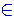
EXP-TIME(d) ).2.3.Logical relations.Logical relations reflect the domain at an analyticallevel. At a semanticallevel they constitute the possible conditional truth statements with respect to the entire domain or parts of it. In logicallanguages these are e.g. truth-value patterns, formulas, propositions, theorems, and the like. They correspond to the columns in the truth-values table. T·(v,d): The set of all possible unique logical relations.Example.With two truth values(v =2, binary system) and two items(d=2), the setT·(v,d) may consist of the following elements (logical relations), represented by proposition symbols and stated in arbitrary order: T·(v=2,d=2)=
{' T' ,' F'
,' A' ,' B' ,'¬A' ,'¬B' ,'( A 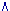 B)' ,'( A B)' ,'( A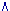 ¬B)' ,'(¬A ¬B)' ,'(¬A
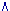 B)' ,'(¬A B)' ,'(¬A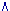 ¬B)' ¬B)','( A  B)' ,'( A B)' ,'( A ¬B)' ,'(¬A ¬B)' ,'(¬A
 B)' ,'(¬A B)' ,'(¬A ¬B)' ¬B)','( A  B)' ,'( A B)' ,'( A#B)' } ).Size.t(v,d) : The total number of possible unique logical relations. The number t(v,d) equals the numer of order variations or permutations with repetition with size (length) b(v,d) from velements.  { {  v v  d
( t(v,d) d
( t(v,d) :=|T·(v,d)|);:= (b1:=1, (b1:=1, ..b(v,d ) )v;:=|B·(v,b(v, d))|;:=v^|B·(v ,d)|;:=v^b(v,d);:=v^(v^d);:=t(v,d -1 )*v ) d, v }.In a binarysystem.Under (v =2 ) applies:T·(v,d) is just as large as the power setof the power setofD·d.The values t(2,d) correspond to the sequence A001146 (formerly M1297, N0497) in the OEIS.  { {  d( t(2,d) d( t(2,d) :=|P·b(2,d)|;:=|P·|P·d||);:=t(2,d-1 )*2;:=A001146(d)|(offset0 ) )d }.
Eg., from (d
={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );follows (t(2,d) ={ 4, 16, 256, 65536, 4294967296, 1.844674407370955 ·(10^19 ), 3.402823669209385 ·(10^38), 1.157920892373162 ·(10^77), 1.340780792994260 ·(10 ^154), 1.797693134862316 ·(10^308),..} ).Range.The number t(v,d) remains hyper-exponential in d.  (2 (2 ≤t(v,d)< 0 ^(
0 ^( 0 ^ 0 ^ 0 ) );
0 ) );
Complexity class.The set T·(v,d) can be searched in hyper-exponential computational time (2-EXP-TIME). ( (T·(v,d)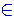
2-EXP-TIME(d) ).2.4.The Truth-values table.Given a domain D·d and value setV·v, the possible immediate logical relations-between-relations are completely defined through the so-called truth-values table .This is construed on basis of systematic value assignment (validation) of the objects by a simple standarized algorithm. The objects each in turn go through the range of values, through so-called 'nested' cycles (loops), thus getting their unique, ordered truth-value patterns. Next, all other ordered value combinations are filled in. In this way a closed, coherent table arises of all possible sequences of (truth) values given parameters (d,v). The value patterns are simular to statementswith at least one proverb, or clause, in other words, 'sentences'. In a binary system, they are expressed by binary numbers. Each of them has length of b(v,d) value constants . These are simular to charactersor symbols in written language. The length b(v,d) equals the amount of information in standard units: bits. Furthermore, the table represents, with perfect garantees, all possible elementary logical relations together with their definite, immediate mutuallogical relations. W·(v,d)[T]: The ordered set of all cells in the truth-values table.Example.Truth value table for a logical system with (v=2) values and (d=2) variables, interpreted for proposition logic ( PPL), predicate logic(PDL), and shorthand Skolemform(Sk) respectively.
Size.w(v,d)t: The total number of cells in the truth-values table. The number w(v,d)t(v,d) becomes the product of the number of domain states (rows) b(v,d), and the number of domain-state relations (columns) t(v,d ):  { {  v v  d
( w(v,d)t d
( w(v,d)t :=|W·( 2,d)t|;:=| ( (T*(v,d) ,B*(v,d))|;:=(|T*(v,d)|*|B*(v,d)|);:=(|B*(v,b(v,d))|*|B*(v,d)|);:=b(v,d)*t(v,d);:=v^(v^d)*v^d;:=v ^((v^d) +d) ) d, v }.In a binarysystem.Under (v =2 ) applies: { {  d( w(2,d)t d( w(2,d)t
:=|W·(2,d)t|;:=2 ^((2 ^d) +d) )d }.
E.g., from (d
Respectively in bytes(8-bits): { 1, 8, 256 ,131072 ,17179869184, 1.475739525896764 ·(10^20
, 5.444517870735015 ·(10^39, 3.705346855594118 ·(10^78, 8.580997075163262 ·(10
^155, 2.301047212623764 ·(10^310, ={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );follows (w(2,d)t ={ 8, 64, 2018, 1048576, 137438953472, 1.180591620717411 ·(10 ^21), 4.355614296588012 ·(10^40), 2.964277484475295 ·(10^79 ), 6.864797660130610 ·(10^156), 1.840837770099011 ·(10^311),..};..} ).2.5.Arguments (Semantic).In setting up an argument we usually don't make use of all possible logicalrelations about the subject in question, but a certain selection, or subset, of T·(v,d).Arguments constitute of unique combinations of logical relations (i.e. without doubles). At a semanticlevel these are sets of conditional truth-value statements which we regard in conjunction. They reflect the domain at a discursivelevel. In logical languages these are sets of truth-value patterns, formulas, propositions, theoremes, and the like: so called ' theories'. For a solid analysis we have to take all possible selections into account. U·(v,d): The set of all possible unique arguments.Example.In an extremely simple, so to say 'primitive' logical system, with two truth values(v =2, binary system ) and only one item(d=1), the setU·(v,d) may consist of the following subsets (arguments), represented here as combinations of logical relations stated in terms of propositiesymbols , and in arbitrary order: U·(v=2,d=1)=
{ {}
,{' T'} ,{' T' ,' F'} {' T' ,' A'} {' T' ,'¬A'} ,{' T' ,' F' ,' A'} ,{' T' ,'F' ,'¬A'} ,{' T' ,' A' ,'¬A'} ,{' T' ,' F' ,' A' ,'¬A'} ,{' F'} ,{' F' ,' A'} ,{' F' ,'¬A'} ,{' F' ,' A' ,'¬A'} ,{' A'} ,{' A' ,'¬A'} ,{¬A'} }. Size.u(2,d) : The total number of possible unique arguments. The number u(2,d) equals the sum of all possible unique unsorted selections (without internal repetition ) from T·(v,d) - i.e. of the binomial coefficients of t( v,d) above the length (number of logical relations) t1 of each subset ofU· v,d. { {  v v  d
( u(2,d)(v,d) d
( u(2,d)(v,d) :=|U·(v,d )|; ( (  u1( ( u1( (U*[ u1] U·(v,d)) ( (u(2,d)(v,d)[u1]
( (u(2,d)(v,d)[u1] :=|U*[u1]|) ( (  t1( (t1 t1( (t1=u(2, d)(v,d)[u1]) ( ( ( (U* [u1] U·t1) (
( U·t1 U·(v ,d)) ) )t1 ) ) )u1 ); ( u(2,d)(v,d) ( u(2,d)(v,d)
:= (u1:=1, (u1:=1, ..u(2,d)( v,d) ) u(2,d)(v,d)[u1];:= (t1:=1, (t1:=1, ..t(v, d) ) (|U·t1|);:= (t1:=1, (t1:=1, ..t(v, d) )binomial(t(v,d), t1);:=|T·(v,t(v,d))|;:=2^|T·(v,d)|;:=2^(v^(v^d)) ) ) d, v }.In a binarysystem.Under (v =2 ) applies:U·(v,d) is just as large as the power setof the power setof the power setofD·d.Some of the values u(2,d)·(2,d) correspond to numbers in the sequence A051285 of the OEIS.  { {  d( u(2,d) d( u(2,d)
Eg., from (d
={1, 2, 3,..} );follows (u(2,d) ={ 16, 65536,1.1579208923731619542357098500868790785327 ·(10^ 77), 2.0035299304068464649790723515602557504478 ·(10^ 19728), 3.1032805438632861402998911558636402031970 ·(10^ 1292913986), 1.9069740116044733845522417467451879838889 ·(10^ 5.553023288523357132 ·(10^ 18) ), 5.4045967703464487690453355840188902868344 ·(10^ 1.0243519943873936375001210925010323270013 ·(10^ 58) ), 3.7925849315209683683886667618408605094478 ·(10^ 3.4856892121032617929865715700930417996503 ·(10^ 76) ), 1.5365619647315663399281284825759039148145 ·(10^ 4.0361523630141126896913151985426995150356 ·(10^ 153) ), 2.3710362762239815690861934492953363891223 ·(10^ 5.4115955659277171970558682351758834358915 ·(10^ 307) ), ..} ).Range.The number u(2,d) remains ultra-exponential in d.  (2 (2 ≤u(2,d)<2 ^( 0 ^(
0 ^( 0 ^ 0 ^ 0 ) ) );
0 ) ) );
Complexity class.The set U·(v,d) can be searched in ultra-exponential computational time (3-EXP-TIME). ( (U·(v,d)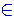
3-EXP-TIME(d) ).2.6.Inference schemes, derivations, (semantic).
(1)
Reasoningas derivation.A very general mode of reasoning which occurs 'in nature' is the one in which at least one thinking step is taken. This means that from a certain collection of data (facts, connections) another set of data is derived. Such a derivation has as its main connective the implication. Briefly, every reasoning has the form 'premiseimplies conclusion'.
Eg.: (X
 Y). Y).
NB. Aristotle formulated a principle for the reasoning form called the syllogism, that is in fact valid for each form of argument:
"The syllogism is a discourse in which, certain things being laid down, another thing follows necessarily, simply because those things are laid down.
" (Aristotle, Prior Anal., 1, 1).
An argument in a system with a scale of vvalues about a domain with dobjects will therefore have the form of
a derivation with the form:
Eg.: (X·(v,d)
In general, we reason from a set of premises (premises) to a collection of conclusions. Y·(v,
d)). Y·(v,
d)). This means that both the premise group as the conclusiongroup consists of a certain subset of This means that both the premise group as the conclusiongroup consists of a certain subset of
U·(v,d).
(a) The premise is shaped by a certain subset from
U·(v,d), sayU·(v,d)[k1] with length (size) l[k1]elements.(b) The conclusion is shaped by some (different or the same) subset say U·(v,d) [k2] with length (size) l[k2]elements.R·(v,d)[k1,k2]: reasoning from (an element of)U·(v,d) to (an element of)U·(v,d) .Broadly speaking, this takes the form:  { {  v v  d d
 k1 k1  k2( k2( R·( v,d)[k1,k2] ( ( U·( v,d)[k1]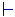 U·(v, d)[k2]) )k2, k1, d, v }.
{
 v1 v1  d1( v1 d1( v1=2; d1=4;D·d1={A, B, C, D};  k1 k1  k2
( ( k2
( (U·(v1,d1)[k1] U·(v1,d1));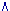 ( (U·(v1,d1)[k2]
U·(v1,d1));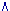 ( (U·(v1,d1)[k1]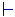
U·(v1,d1)[k2]);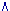 ( (U·(v1,d1)[k1]={A, (B ¬C) }; ¬C) };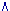 ( (U·(v1,d1)[k2]={¬A B), (C B), (C ¬D) } ); ¬D) } );
 R·(v,d)[k1,k2]:=((A, (B ¬C) ) ¬C) ) 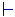 (
¬A (
¬A B), (C B), (C ¬D) ) )k2
, k1 )d1, v1 }. ¬D) ) )k2
, k1 )d1, v1 }.(2) De verzamelingvan afleidingen.R·(v,d)[U]: the set of all possible unique inferences or conclusions at the semanticlevel. { {  v v  d
( d
( R·(v,d)[U]:= (k1:=1,
(k1:=1, ..u(v,d) ) (k2
:=1, (k2
:=1, ..u(v,d) )R·(v,d) [U][k1,k2] k2, k1 )d , v }. This means that the set of all possible uniqueforms of reasoning under the parameters {
v,d} is formed by a matrix: This means that the set of all possible uniqueforms of reasoning under the parameters {
v,d} is formed by a matrix: { {  v v  d
( d
( R·(v,d)[U]:=(U·(v,d)XU·(v,d) ) ) d, v }.Size.r(v,d)U: The total number of possible unique inferencesor conclusions at the semantic level.  The size of the collection is of course formed by the Cartesian product (
u(2,d) ·u(2,d)). The size of the collection is of course formed by the Cartesian product (
u(2,d) ·u(2,d)). { {  v v  d
( r(v,d)U d
( r(v,d)U :=|R·(v ,d)[U]|;:=u(v,d)^2 ;:=v^(2*t(v,d) ) )d , v }.In een binairsysteem. { {  d( r(2,d)U d( r(2,d)U :=|R·(2,d)[U]|;:=u(2,d)^2;:=2^(2*t( 2,d) ):=)d, v }.
Bijv., bij (d
={1, 2, 3,..} );volgt (r(2,d)U ={ 256, 4294967296, 1.340780792994 ·(10^154 ),..} ).Complexity class.The set R·(v,d)[U]: remains on the same complexity level asU·(v,d).(2) Derivations are at semanticlevel bipartite.As mentioned, a collection U·(v,d) contains subsetsU·(v,d)[k1] each consisting of unique combinations of logical relations from the collectionT·(v,d). All those elements have their own logical validity value which is unique withinT·(v,d). When we combine these values, for example in a premiseor conclusion within a derivation, then according to the logical laws at semanticlevel, the immediate result is paraphrasereduction of the combination to one logical validity value which in turn corresponds to one logical relation inT·(v,d). This means that as a net result, premiseand conclusioneach contain (again: at semanticlevel) only one element. Therefore, at semantic level we can calculate logical derivations as propositionswith only two simple elements.2.7.Minimal inferences, derivations (Semantic).
(1)
The setof reasonings in their minimalparaphraseform.Each of the subsets in the two components of the derivation can therefore always be reduced according to logical laws to the smallest possible logical-semantic content: in this case, logical relations in a domain with dobjects. We consider the components as mentioned in conjunction. For convenience, we assume a binarysystem. This always has two values: valence
(v
This system has a number of logical relationships as we saw earlier:=2 ).
(t(v,d)
=v^(v^d)). The set of possible arguments can therefore be reduced to its paraphrase reduct
versionat semanticlevel. The set of possible arguments can therefore be reduced to its paraphrase reduct
versionat semanticlevel.R·(v,d)[T] the set of all possible uniqueminimal reasoning or conclusions at semanticlevel. (v d (v d |( k1 k1  k2(
k2( R·(v,d)[U][k1,k2 ] ( (U·(v,d)[k1] in conjunctie U·(v,d)[k2] in conjunctie ); ( (Cj(U·(v,d)[k1 ] Cj(U·(v,d) [k2]); ( (U·(v,d)[k1]synpar-rdc U·(v,d )[k2]synpar-rdc); par-rdc( p1 p1  q1( (
q1( (T·(v,d)[p1]
T·(v,d)[q1]); R·(v,d)[T] [p1,q1] ; R·(v,d)[T]:= (p1:=1, (p1:=1, ..u(2,d) ) (q1:=1,
(q1:=1, ..u(2,d) )R·(v,d) [T][p1,q1] ) ) ); The paraphrase reductversionsof premiseand conclusion will therefore each consist of exactly one element from each of the original subsets
k1, k2, from The paraphrase reductversionsof premiseand conclusion will therefore each consist of exactly one element from each of the original subsets
k1, k2, from U·(v,d). This means that the set of all possible uniqueminimalforms of reasoning under the parameters
{v,d} is formed by a matrix: This means that the set of all possible uniqueminimalforms of reasoning under the parameters
{v,d} is formed by a matrix: { {  v v  d
( d
( R·(v,d)[T]:=(T·(v,d)XT·(v,d) ) ) d, v }.Size.r(v,d)T: The total number of all possible unique minimal reasoning or conclusions.  Obviously, the size of this collection is formed by the Cartesian product (
t(v,d) ·t(v,d)). Obviously, the size of this collection is formed by the Cartesian product (
t(v,d) ·t(v,d)). { {  v v  d
( r(v,d)T d
( r(v,d)T :=|R·(v ,d)[T]|;:=t(v,d)^2 ;:=v^(2*b(v,d) ) )d , v }.In a binarysystem. { {  d( r(2,d)T d( r(2,d)T :=|R·(2,d)[T]|;:=t(2,d)^2;:=t(2,d+1);:=2^(2*b(2,d) ):=A001146(d)^2;:=A001146(d+1 ) )d }.
Eg., from (d
={ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );follow quantities of tupuls for derivation relations (r(2,d)T =1.844674407370955 ·(10 ^19), 3.402823669209384 ·(10^38), 1.157920892373162 ·(10^77 ), 1.340780792994260 ·(10^154), 1.797693134862316 ·(10^308), 3.231700607131101 ·(10 ^616),..} ).Complexity class.The set R·(v,d)[T]: remains on the same complexity level asT·(v,d).(2) Evaluationof arguments.Ultimately, we want to know whether an argument is valid, in other words valid. In other words, which of the derivation relations from the matrix R·(v,d)[T] are valid?Each element of the matrix R·(v,d)[T] is easy to solve like any implication according to the rules of the general truth value table.
See above, 2.4. Truth value table.
Also see: Principles of Logical Proof; (4.1a) Method of Truth Value Tables. And: Proof Method for Proposition Logic: the Truth Value Table method .
(2.1)
Encodingas binary numbers.Each of the logical relationships in the components of R·(v,d)[T] can be endoded in the simplest logical system, propoposition logic (PPL), as a binary truth value pattern.Each of these value patterns is an element of the set (value patterns of) logical relationships T·( v,d)[k1].This means, as we have seen, that each of these binary patterns has a length of:
b(v,d)·(v,d)
(2.2) =v·^d .Paraphrase reduction to one binary number.The results again consist of binary truth value patterns. (2.3) Interpretation of the binary outcome.Rules for interpretation of a binary truth value pattern:
(a) Not all bits are set to 0 or 1 : undecided, indefinite contingency.
(b) All bits are set to 0 or 1 : decided.
(b1) All bits are set to 0: contradiction (non-satisfiability).
Only true if 'true implies false' (i.e. $1 $0 ).(b2) Not all bits are set to 0, and neither are they to 1 : (definitite) contingency.
(b2.1) Not all bits are set to 0 : consistency (satisfiability).
(b3) All bits are set to 1: validity.(b2.2) Not all bits are set to 1 : invalidity (presupposition, c.q. fallacy). (3) Validreasonings.The total number of all possible unique contradictoryreasoning or conclusions is simply the same as that of any set of disjunctions: exactly one. The total number of all possible unique consistentreasoning or conclusionsis therefore simply r(v,d) ·(v,d)T-1. Size.xT: The total number of all possible unique validreasonings or conclusions. The formula for the number of valid derivation relations xTwith valence v=2 and number of objects dis:
xT·(v,d)
=(v+1)·^b (v,d);=(v+1)·^(v·^d);In a binarysystem.The values xT·(2,d) largely correspond to the powers of 3 of the powers of 2. See sequence A011764 in the OEIS.
Eg., under (v
Same range as percentages of valid implications:=2 );from (d ={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..} );folow as quantities of valid implications: { 9, 81, 6561, 43046721, 1.853020188851841 ·(10 ^015), 3.433683820292512 ·(10 ^030 ), 1.179018457773858 ·(10 ^061), 1.390084523771447 ·(10 ^122), 1.932334983228892 ·(10 ^244), 3.733918487410200 ·(10 ^488), .. }.
{ 56.25 31.640625 10.01129150 390625 1.002259575 761855 1.004524257 206333 ·(10 ^-002) 1.009068983 315935 ·(10
^-006) 1.018220213 090254 ·(10 ^-014) 1.036772402 345563 ·(10 ^-030
) 1.074897014 265390 ·(10 ^-062) 1.155403591 276649 ·(10 ^-126) .. } );
(4) Table.Below is a table with the most important dimensions of the collections mentioned above.
This table shows how combinatorial possibilities in a simple logical system quickly lead to a search space of astronomical proportions. For example, with 100000 itemswe can make a number of 'minimal arguments' (at the semantic level) whose number consists of a number of digits where just the lengthof the number can be represented with an exponent (decimal logarithm) which in turn has a length of 30102 digits. In other words, not the number itself is 30102 digits long, but the exponent with which her length can be represented. (5) For comparision.To put the above numbers somewhat in perspective, the following are some examples of large numbers occurring in nature (all according to fairly rough estimates). In the universe.• The number of galaxy clusters: approx. 4 ·10 ^8. • The number of galaxies in the universe: approx. 10 ^11. • The number of stars per galaxy: approx. 10^8to 10^14. • The number of stars in 'our' galaxy, the Milky Way: approx. 10^11. • The number of stars in the observable universe: approx. 10 ^22. • The number of molecules in the observable universe: approx. 10 ^80. On Earth.• The total number of fish in the oceans: approx. 3.5 ·10 ^9. • The number of ants on Earth: approx. 3.5 ·10 ^12. • The total number of grains of sand on all beaches on earth: approx. 10 ^21. In the human body.• The number of cells in the human body: approx. 10 ^14. • The number of different proteins that can be built from 100 amino acids: approx. 10 ^130. To highlight two examples: With 5 items, you can make almost as many -unique, minimal- arguments as the total number of grains of sand on all beaches on Earth. With 7 items, which is the average memory capacity of our conscious attention window, you can make almost as many -unique, minimal- arguments as molecules existing in the observable universe. These -literally- astronomical numbers indicate the level of complexity and thus decision problems. It does not help to resort to a more advanced logical system. As a general rule, the more advanced the logical system, the more expressive power it has, but the less decision-making power. With each step towards a more advanced logical system, such as modal logic, multivalued logic, predicate logic, etc., and also so-called 'fuzzy logic', the numbers and problems of complexity and decidability are only increasing explosively again! Clearly, without sufficient knowledge and skills of logical proof and testing, possible arguments about more than two items are already almost impossible to assess. C.P. van der Velde © 2014, 2018. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||